だれしも複利効果に狙ってロットを調整し、トレードの資金を急速に増やしたいと思うでしょう。
その時、1回あたり資金をどれくらい投入すればいいか決めるこのオプティマルfです。これを感覚ではなく数式で決めることができます。
この記事ではなるだけ簡単にこのオプティマルfを求める方法を説明します。
ですがこれを提唱している「ラルフ・ビンズ」が書いた本を読んだほうがはっきり理解できるかと思うので以下を読むことを本当はおすすめします。(笑)
この記事はこの本をもとに書いています。
オプティマルfの式
まずだらだら説明してもあれなので手っ取り早く式を書いておきます。
トレード全体の幾何平均利益 =
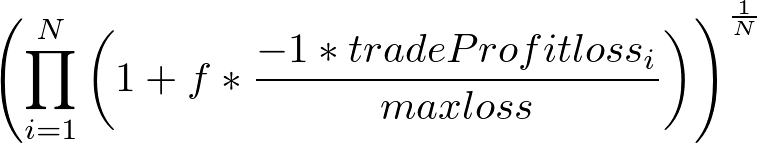
tradeProfitloss_i =
ポジションごとの損益の数列(-1万円, +2万円, +3万円, -3万円……など)
maxloss =
トレードを通しての最大損失
N=
トレード回数
Π : 総乗。数列全体を以下のようにかけ合わせたものになります。
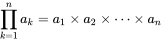
この式のfと幾何平均以外はすでにわかっている数字なのでこの式(幾何平均利益) を最大化する数値fを求めるのがオプティマルfの求め方です。
オプティマルfの使い方・求め方を例をあげて解説
オプティマルfの求め方は、基本的は総当りで上の式のfに0から1まで数字を入れていき、式が最大になったときのfがオプティマルfになります。
もしくは上の式の総乗Πが最大になるときですね。
求め方はめんどくさいと思いますが(笑)
エクセルやプログラムや関数電卓などどれか使えるものを使って求めてください。
求め方の例
まず、以下のようにトレード損益(トレードした結果)があるとします。
9, 18, 7 , 1, 10, -5, -3, -17 , -7
(損益の値が少ないので単位はドルで考えてください。)
まずトレードを通しての最大損失はひと目見て「-17」ということがわかるでしょう。
ちなみにfは0から1の値を取ります。
次に、fに0.1刻みで代入して上記式を求めます。
| トレード損益 | 1 + f × (-1 × 損益÷最大損失) f=0.1 |
| 9 | 1.052941 ≒1 + 0.1×(-1×9÷ -17) |
| 18 | 1.105882 |
| 7 | 1.041176 |
| 1 | 1.005882 |
| 10 | 1.058823 |
| -5 | 0.970588 |
| -3 | 0.982352 |
| -17 | 0.9 |
| -7 | 0 .958823 |
| Π | 上を全部かけると1.062409 =1.052941 × 1.105882 × …..× 0 .958823 |
| トレード損益 | 1 + f × (-1 × 損益÷最大損失) f=0.2 |
| 9 | 1.105882 |
| 18 | 1.211764 |
| 7 | 1.082352 |
| 1 | 1,011764 |
| 10 | 1.117647 |
| -5 | 0.941176 |
| -3 | 0.964705 |
| -17 | 0.8 |
| -7 | 0 .958823 |
| Π | 上を全部かけると 1.093231 |
| トレード損益 | 1 + f × (-1 × 損益÷最大損失) f=0.3 |
| 9 | 1.158823 |
| 18 | 1.317647 |
| 7 | 1.123529 |
| 1 | 1.017647 |
| 10 | 1.176470 |
| -5 | 0.911764 |
| -3 | 0.947058 |
| -17 | 0.7 |
| -7 | 0.876470 |
| Π | 上を全部かけると 1.088113 |
0.1刻みで代入し、上表の Π (幾何平均利益^N, 表右側をかけたもの)が上昇から下降に転じている範囲は0.2<f<0.3となっています。
オプティマルfを0から代入した場合、本によれば式の結果は上昇から下降に転じるようです。
実際に横軸fでグラフを描写するとfが0から1の範囲で利益が曲線を描き上昇から下降に転じています。
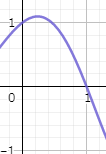
このサイトに入力するとグラフが見られます。
オプティマルfは0.2から0.3にあるようなので、次は0.01刻みでfに代入します。
| トレード損益 | 1 + f × (-1 × 損益÷最大損失) f=0.25 |
| 9 | 1.132352 |
| 18 | 1.264705 |
| 7 | 1.102941 |
| 1 | 1.014705 |
| 10 | 1.147058 |
| -5 | 0.926470 |
| -3 | 0.955882 |
| -17 | 0.75 |
| -7 | 0.897058 |
| Π | 上を全部かけると 1,095387 = 1.132352 × 1.264705 × 1.102941 … ×0.897058) |
| トレード損益 | 1 + f × (-1 × 損益÷最大損失) f=0.23 |
| 9 | 1.121764 |
| 18 | 1.243529 |
| 7 | 1.094705 |
| 1 | 1.013529 |
| 10 | 1.135294 |
| -5 | 0.932352 |
| -3 | 0.959411 |
| -17 | 0.77 |
| -7 | 0.905294 |
| Π | 上を全部かけると 1.095634 |
| トレード損益 | 1 + f × (-1 × 損益÷最大損失) f=0.24 |
| 9 | 1.127058 |
| 18 | 1.254117 |
| 7 | 1.098823 |
| 1 | 1.014117 |
| 10 | 1.141176 |
| -5 | 0.929411 |
| -3 | 0.957647 |
| -17 | 0.76 |
| -7 | 0.901176 |
| Π | 上を全部かけると 1.095698 |
上の表からf=0.24のとき、上を全部かけると~が最大になることがわかります。そして式が最大の値((1.095698)^(1/9) =1.010206)を取ることがわかります。
ですのでこの一連のトレードのオプティマル fは0.24になります。
※もっとプログラムやpythonでいい求め方があるならむしろ教えて下さい。
オプティマルfの使い方
オプティマルfは資産に何%かけるかを示すものと誤解されがちですが、
実際には、総資産を( 最大損失÷-1 * オプティマルf)で割った答えが枚数や売買単位になります。
上の例だと、
-17 ÷ -0.24 = 70.83
となり70.83ドルあたり1単位をかければいいことになります。
上の表の損益がすべて0.01lot(1lot=10万ドル)を売買したときの損益であるならば、70.83ドルあたり0.01lotをかければいいということになります。
1000ドル持っているならば、1000 ÷ 70.83 = 14
つまり0.14lot(売買単位)取引すればいいということになります。
オプティマルfの求め方の流れ・まとめ
1)一連のトレード損益(トレードした結果)を用意する。
※トレードした個々の損益はすべて同じ枚数にそろえなければいけませんので、各損益を売買単位で割った数列を用意してください。
例えば1lotで+10,次に2lotで-8損益が出た場合は +10, -4とする。
2) 1 + f × (-1 × 損益÷最大損失) を使う。
個々の損益を当てはめて計算してすべて掛け算する。
fには0から1までの数字を入れて繰り返しすべてかけたものが最大になればそれがオプティマルfになります。
実際に手で求めるのは大変なので、エクセルがプログラムを書いて求めてください。
オプティマルfの注意点
まず利益が出るストラテジー・手法であることが前提
このオプティマルfはプラスの利益を最大化するものであって、マイナスをプラスの利益へと変えることは無理です。
優位性があるストラテジー・EA・手法を用意した上で計算してください。
(この前提条件が一番難しいかと思いますが)
一回一回のトレードが独立試行であること
つまり前のトレードが今のトレードに影響するものであればおそらくオプティマルfは適用できません。
たとえばドテンとかマーチンゲールとかですかね。
場合によっては使う場合はfを調整する
オプティマルfは最大リスクを取れる値としての意味合いがあり、オプティマルfが大きければそれだけドローダウンが大きくなります。
もし10000円をオプティマルf0.6で取引するならば、最大損失の予想額は6000円になります。
オプティマルfはリスクを取りすぎている場合があるため、fを半分にするなど、心理的かつ投下する市場に耐えられる値にオプティマルfを調整してください。
ケリーの公式とオプティマルfは厳密には別物
ケリーの公式とオプティマルfは別物です。
ケリーの公式は利益が常に同額で損失が常に同額である場合に使えます。
まとめ
自分は数学者ではないのでなんでこうなるかとか理由はこの記事では書いていませんので、もっと理解を深めたれば本を読むことを強くおすすめします。
この本を読む価値は十分にあります。
以上、本の宣伝でした。




コメント